문제 분석
https://www.acmicpc.net/problem/16118
16118번: 달빛 여우
첫 줄에 나무 그루터기의 개수와 오솔길의 개수를 의미하는 정수 N, M(2 ≤ N ≤ 4,000, 1 ≤ M ≤ 100,000)이 주어진다. 두 번째 줄부터 M개의 줄에 걸쳐 각 줄에 세 개의 정수 a, b, d(1 ≤ a, b ≤ N, a ≠ b
www.acmicpc.net
- 다익스트라를 구현할 줄 안다면 여우의 이동 경로는 어렵지 않게 구할 수 있다.
- 그러나 늑대의 이동경로를 구하는 데서 약간 아이디어가 필요하다.
- 늑대는 각각의 그루터기에 늦게 도착하거나 빠르게 도착할 수 있다. 이 때 단순 다익스트라 처럼 구현한다면 이전 최단 경로에 비해서 이번에 비교하는 최단 경로가 더 짧다면 갱신을 해줄텐데, 이 문제에선 그렇게 생각하면 앞선 경로에서 누락되는 부분이 생긴다.
- 예를 들어, 아래 그림에서 5번 경로에 갈 때 1-3-5 보다 1-2-3-5를 거쳐 가는게 더 빠름에도 불구하고, 1-3과 1-2-3을 비교하는 구간에서 1-3이 더 빠르다는 이유로 3번 노드를 결정할 때 해당 경로는 제외가 되어버린다. 여우의 이동경로를 구할 땐 속도가 변화되는 일이 없으니 매 구간을 그대로 더해주면 되지만, 늑대의 이동경로를 구할 때는 각 노드에 빠르게/느리게 도착하느냐에 따라서 출발점~노드까지의 최단경로가 변화될 수 있는 것이다.
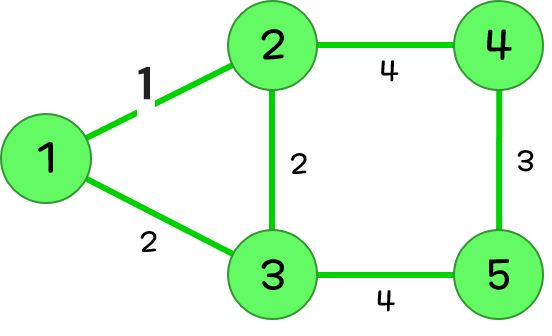
- 따라서 늑대의 경로를 구할 때는 각각 노드에 느리게 도착할 때/빠르게 도착할 때를 모두 저장해두고, 나중에 둘을 비교해서 더 빠른 값을 반환하면 된다. DP와 다익스트라를 합친 느낌이라고 보면 될듯?
코드
import sys
from heapq import heappush,heappop
from collections import defaultdict
input = sys.stdin.readline
INF = sys.maxsize
def dijk_fox():
dist=[INF]*(N+1)
dist[1]=0
heap=[]
heappush(heap,(dist[1],1))
while heap:
cur_dist,cur_node= heappop(heap)
if dist[cur_node] < cur_dist: #더 나중에 들어온 값중에 더 낮은 가중치를 가진 경로가 있었다면 pass
continue
#인접 노드 중에 위 노드를 거쳤을 때 더 짧아지는 값이 있다면 값을 갱신해줌.
for new_dst, new_dist in graph[cur_node].items():
accumulate_dist= cur_dist+new_dist
if accumulate_dist < dist[new_dst]:
dist[new_dst]=accumulate_dist
heappush(heap,(accumulate_dist,new_dst))
return dist
def dijk_wolf():
#빠르게 도착하는 경우 dist[0][x], 느리게 도착하는 경우 dist[1][x]
dist= [[INF] * (N+1) for _ in range(2)]
dist[1][1]=0
q=[]
heappush(q,(dist[1][1],1,False)) #노드 1에 느리게 도착 - 다음 노드 부터는 빠르게 도착함.
while q:
cur_dist,cur_node,cur_speed=heappop(q)
if cur_speed and dist[0][cur_node] < cur_dist:
continue
elif not cur_speed and dist[1][cur_node]<cur_dist:
continue
for new_dst,new_dist in graph[cur_node].items():
accumulate_dist = cur_dist
if not cur_speed: #이번에 느리게 도착했다면, 인접 노드에서 빠르게 도착해야 함. (2,3번 노드 갈 때 빠르게 도착)
accumulate_dist+=new_dist//2
if accumulate_dist < dist[0][new_dst]:
dist[0][new_dst]=accumulate_dist
heappush(q,(dist[0][new_dst],new_dst,True)) #이제 느리게 가야함
else: #빠르게 도착했으므로, 느리게 출발
accumulate_dist+=new_dist*2
if accumulate_dist < dist[1][new_dst]:
dist[1][new_dst]=accumulate_dist
heappush(q,(dist[1][new_dst],new_dst,False))
return dist
N,M = map(int,input().split())
graph= defaultdict(dict)
for _ in range(M):
x,y,w=map(int,input().split())
graph[x][y]=w*2
graph[y][x]=w*2
fox_dist = dijk_fox()
wolf_dist= dijk_wolf()
ans=0
for i in range(1,N+1):
if fox_dist[i] < min(wolf_dist[0][i],wolf_dist[1][i]):
ans+=1
print(ans)'Computer Science > 알고리즘(백준+프로그래머스)' 카테고리의 다른 글
| 백준 1238) 파티_Python (0) | 2022.11.02 |
|---|---|
| 백준 1520) 내리막길_Python (0) | 2022.10.27 |
| 백준 17144) 미세먼지 안녕!_Python (0) | 2022.07.08 |
| 백준 14501) 퇴사_ Python (0) | 2022.07.01 |
| 백준 12865) 평범한 가방 - Python (0) | 2022.06.12 |
